四重加密
下载附件后,得到一个rar文件,发现被加密,无法解压
使用Bandizip打开

注释中有段编码OFZW4Y3UMY======
CyberChef
base64解码得到第一层压缩包密码

qsnctf
打开后有一个文本文档

内容如下
zcye{mxmemtxrzt_lzbha_kwmqzec}|key=hello
NCR,HTML解码
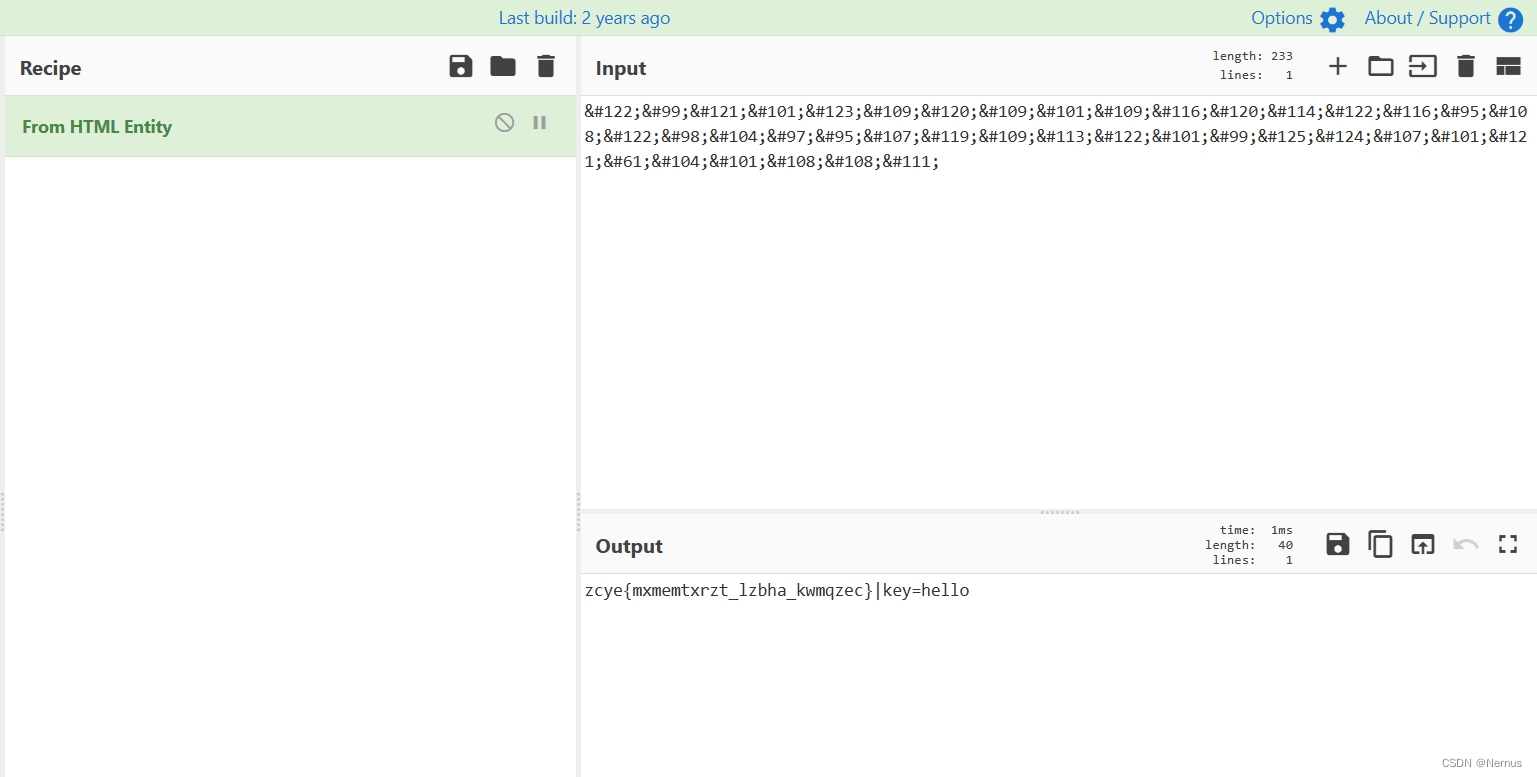
得到一串密文和key
zcye{mxmemtxrzt_lzbha_kwmqzec}|key=hello
维吉尼亚解码
维吉尼亚加密/解密 - Bugku CTF

得到synt{yqitbfqnoi_xsxwp_wpifoqv}
根据题目提示四重加密,应该还有一层
ROT13解码
CTF在线工具-在线Rot13密码加密|在线Rot13密码解密|Rot13密码算法|Rot13 Cipher (hiencode.com)
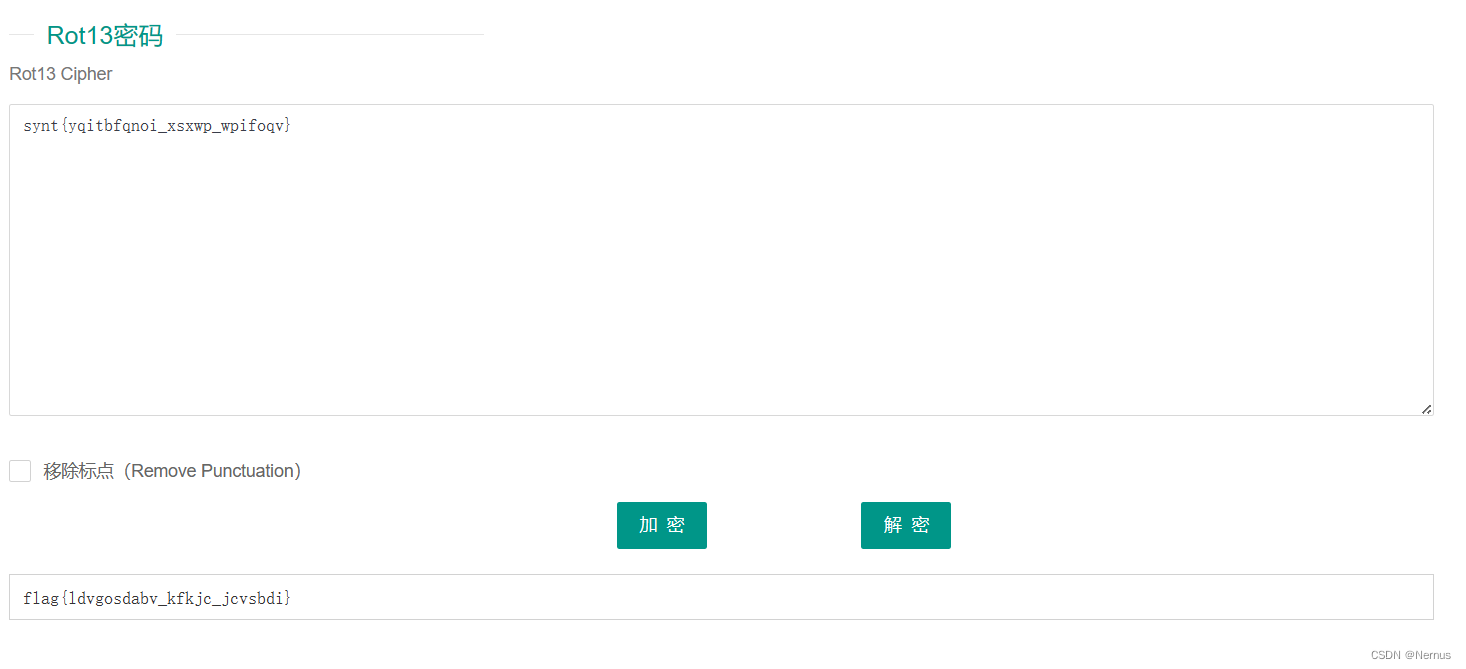
得到flag
根据题目要求改下壳
qsnctf{ldvgosdabv_kfkjc_jcvsbdi}
factor1

下载解压,打开附件查看

维纳攻击(特点是e超级大)
e超级大,先求出d,然后e,n,d已知,求p,q
可以分为两部分代码:
给 e,n,求出 d
import gmpy2
import libnum
import hashlib
import random
def continuedFra(x, y):
cf = []
while y:
cf.append(x // y)
x, y = y, x % y
return cf
def gradualFra(cf):
numerator = 0
denominator = 1
for x in cf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return numerator, denominator
def solve_pq(a, b, c):
par = gmpy2.isqrt(b * b - 4 * a * c)
return (-b + par) // (2 * a), (-b - par) // (2 * a)
def getGradualFra(cf):
gf = []
for i in range(1, len(cf) + 1):
gf.append(gradualFra(cf[:i]))
return gf
def wienerAttack(e, n):
cf = continuedFra(e, n)
gf = getGradualFra(cf)
for d, k in gf:
if k == 0: continue
if (e * d - 1) % k != 0:
continue
phi = (e * d - 1) // k
p, q = solve_pq(1, n - phi + 1, n)
if p * q == n:
return d
e=4602579741478096718172697218991734057017874575484294836043557658035277770732473025335441717904100009903832353915404911860888652406859201203199117870443451616457858224082143505393843596092945634675849883286107358454466242110831071552006337406116884147391687266536283395576632885877802269157970812862013700574069981471342712011889330292259696760297157958521276388120468220050600419562910879539594831789625596079773163447643235584124521162320450208920533174722239029506505492660271016917768383199286913178821124229554263149007237679675898370759082438533535303763664408320263258144488534391712835778283152436277295861859
n=78665180675705390001452176028555030916759695827388719494705803822699938653475348982551790040292552032924503104351703419136483078949363470430486531014134503794074329285351511023863461560882297331218446027873891885693166833003633460113924956936552466354566559741886902240131031116897293107970411780310764816053
d=wienerAttack(e, n**2)
print('d=',d)
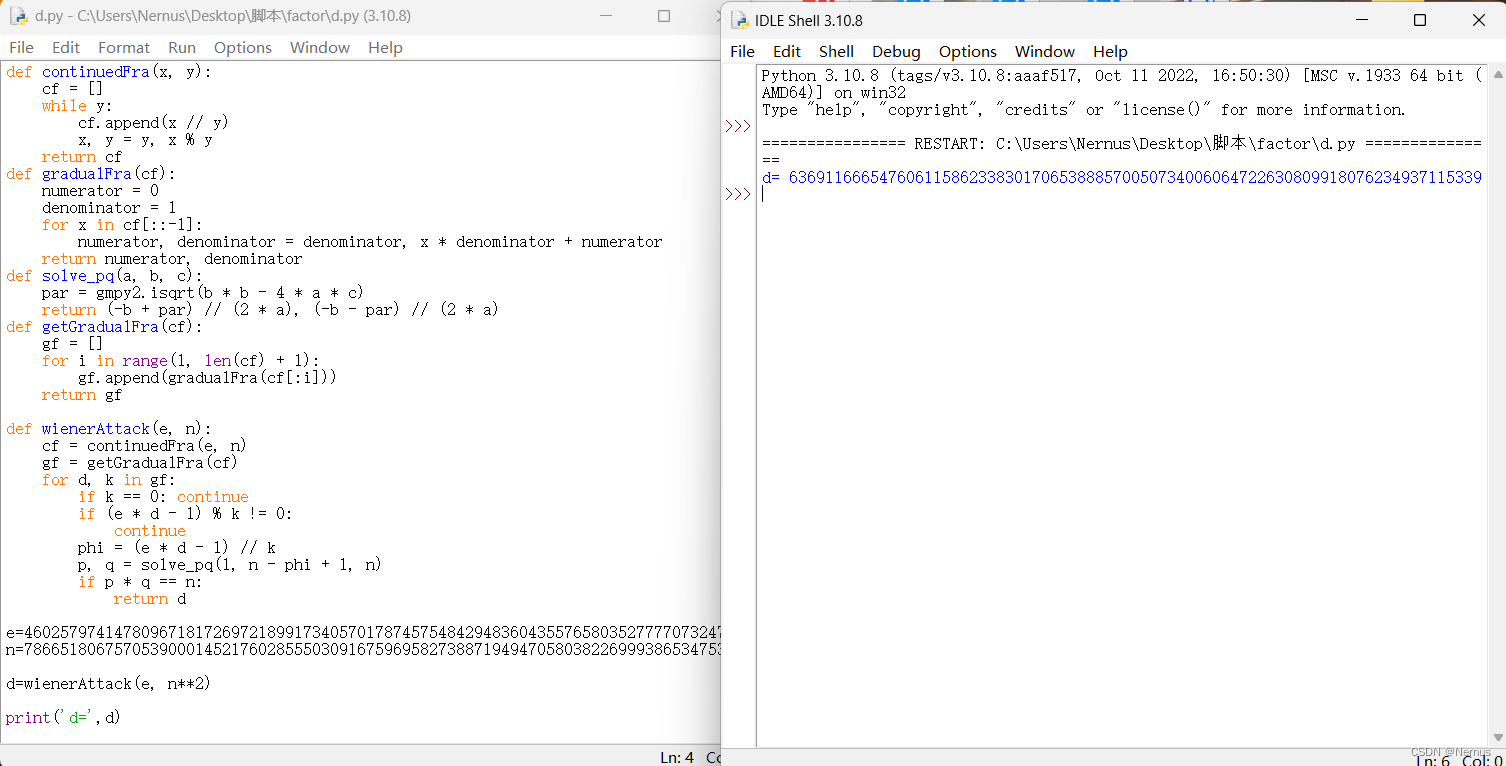
运行后得到d
#d= 63691166654760611586233830170653888570050734006064722630809918076234937115339
因此 e,n,d 已知,求出flag
import gmpy2
import libnum
import hashlib
import random
e=4602579741478096718172697218991734057017874575484294836043557658035277770732473025335441717904100009903832353915404911860888652406859201203199117870443451616457858224082143505393843596092945634675849883286107358454466242110831071552006337406116884147391687266536283395576632885877802269157970812862013700574069981471342712011889330292259696760297157958521276388120468220050600419562910879539594831789625596079773163447643235584124521162320450208920533174722239029506505492660271016917768383199286913178821124229554263149007237679675898370759082438533535303763664408320263258144488534391712835778283152436277295861859
n=78665180675705390001452176028555030916759695827388719494705803822699938653475348982551790040292552032924503104351703419136483078949363470430486531014134503794074329285351511023863461560882297331218446027873891885693166833003633460113924956936552466354566559741886902240131031116897293107970411780310764816053
d= 63691166654760611586233830170653888570050734006064722630809918076234937115339
k = e * d - 1
r = k
t = 0
while True:
r = r // 2
t += 1
if r % 2 == 1:
break
success = False
for i in range(1, 101):
g = random.randint(0, n)
y = pow(g, r, n)
if y == 1 or y == n - 1:
continue
for j in range(1, t):
x = pow(y, 2, n)
if x == 1:
success = True
break
elif x == n - 1:
continue
else:
y = x
if success:
break
else:
continue
if success:
p = libnum.gcd(y - 1, n)
q = n // p
print ('P: ' + '%s' % p)
print ('Q: ' + '%s' % q)
hash_result = hashlib.md5(str(p + q).encode()).hexdigest()
print(b'qsnctf{' + hash_result.encode() + b'}')
#qsnctf 注意格式问题
else:
print ('Cannot compute P and Q')
运行
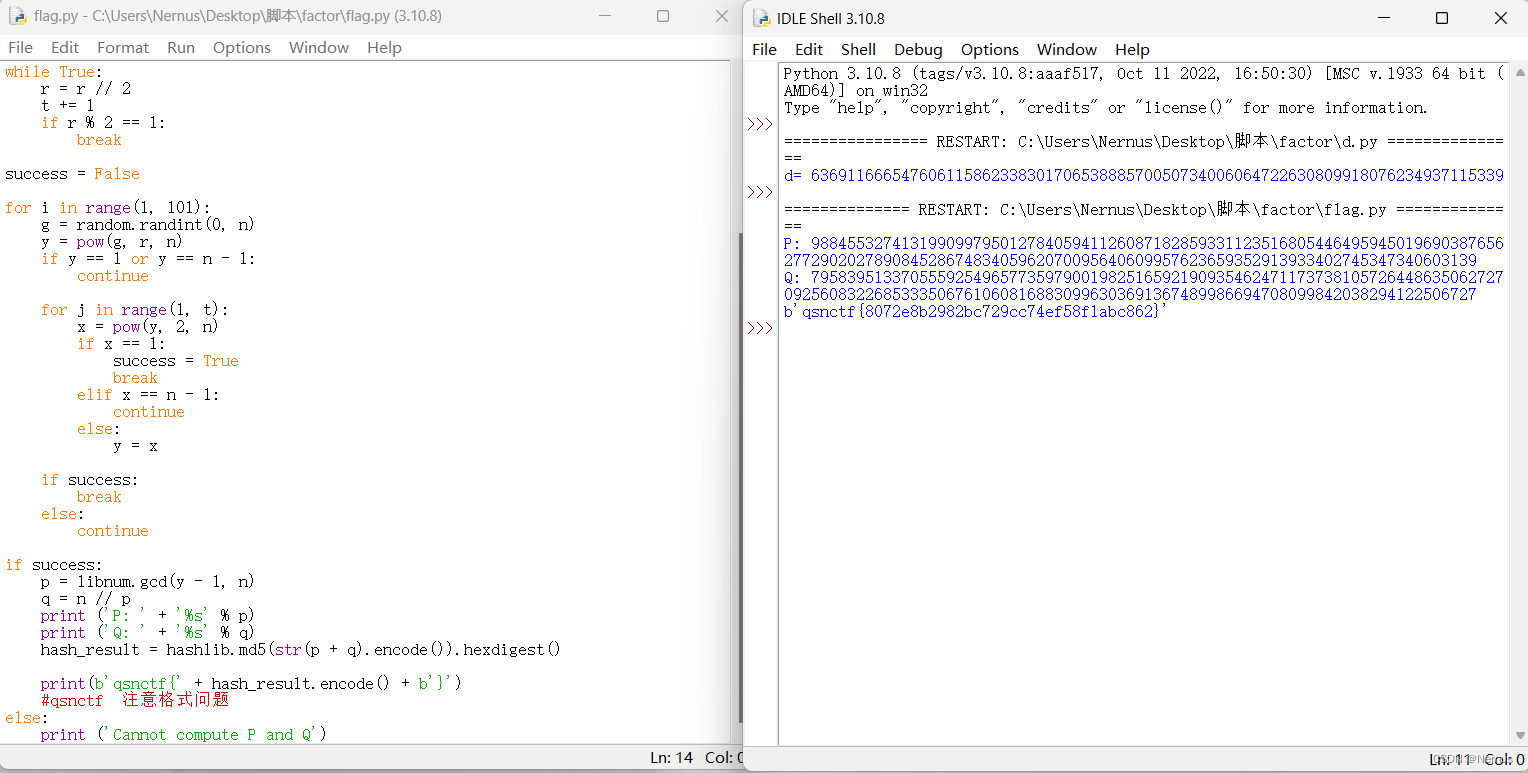
得到flag
qsnctf{8072e8b2982bc729cc74ef58f1abc862}
凯撒大帝的征讨之路
下载解压,打开附件

lnixoa{1x2azz7w8axyva7y1z2320vxy6v97v9a}
使用在线工具,枚举解密后,观察前缀
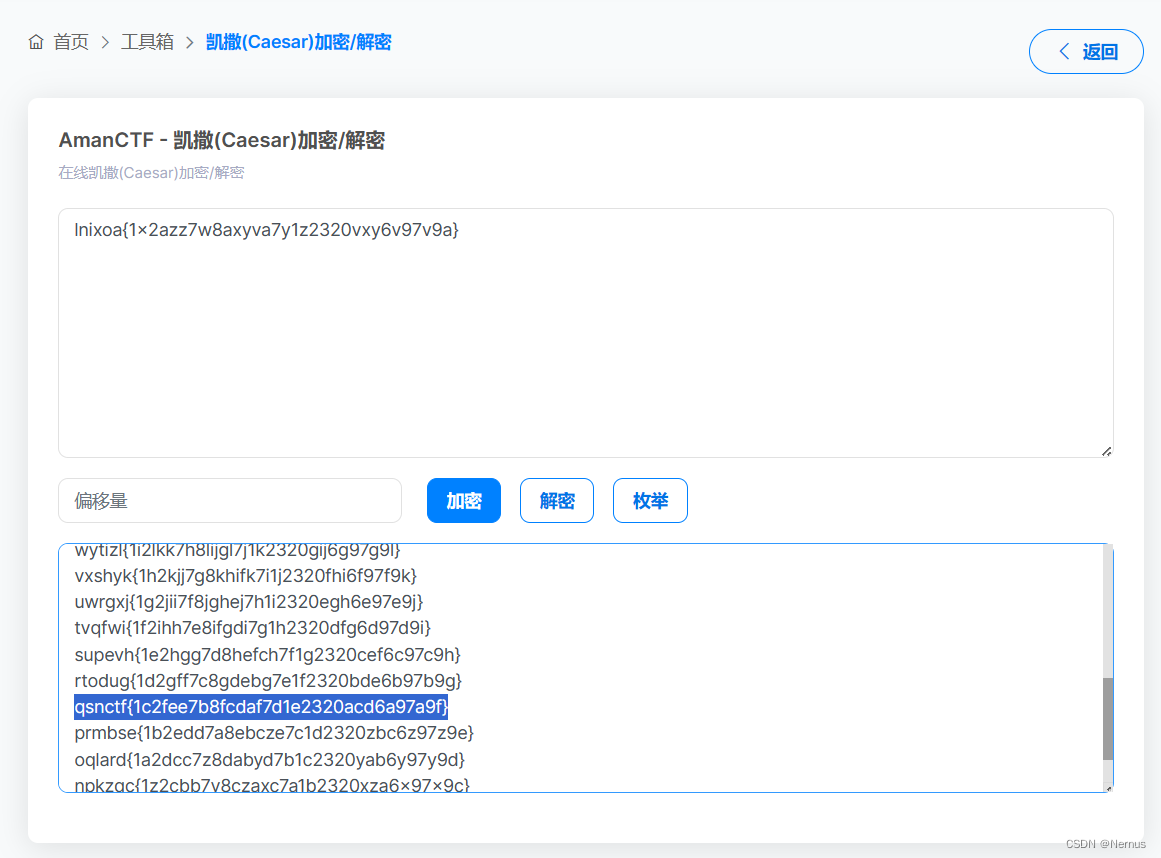
得到flag
qsnctf{1c2fee7b8fcdaf7d1e2320acd6a97a9f}
也有大佬编写脚本
import base64
def caesar_decrypt(ciphertext, shift=ord('l')-ord('q')):
str_list = list(ciphertext)
i = 0
while i < len(ciphertext):
if str_list[i].isalpha():
a = "A" if str_list[i].isupper() else "a"
str_list[i] = chr((ord(str_list[i]) - ord(a) - shift) % 26 + ord(a))
i += 1
return ''.join(str_list)
str='lnixoa{1x2azz7w8axyva7y1z2320vxy6v97v9a}'
kstr = caesar_decrypt(str)
print( kstr)
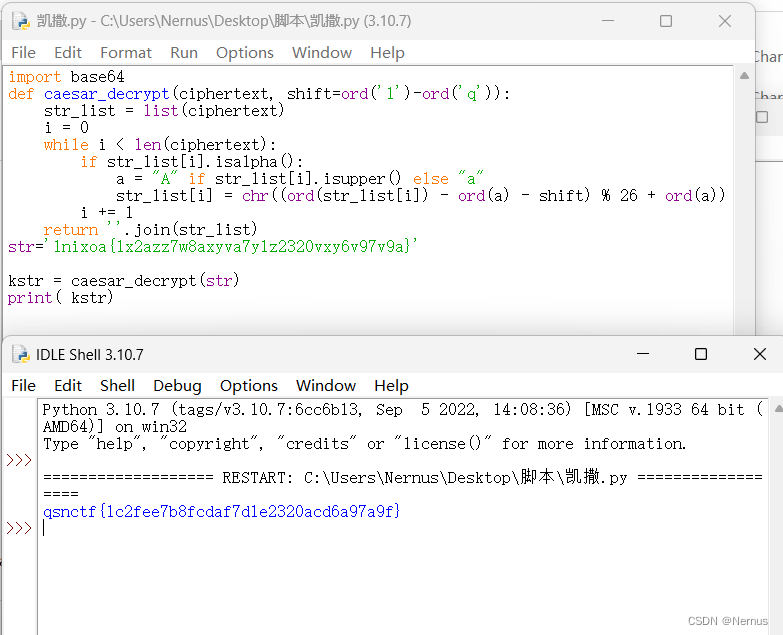
运行得到flag
PigPig
解压打开文件
![]()
明显,猪圈密码
猪圈密码解密-ME2在线工具 (metools.info)
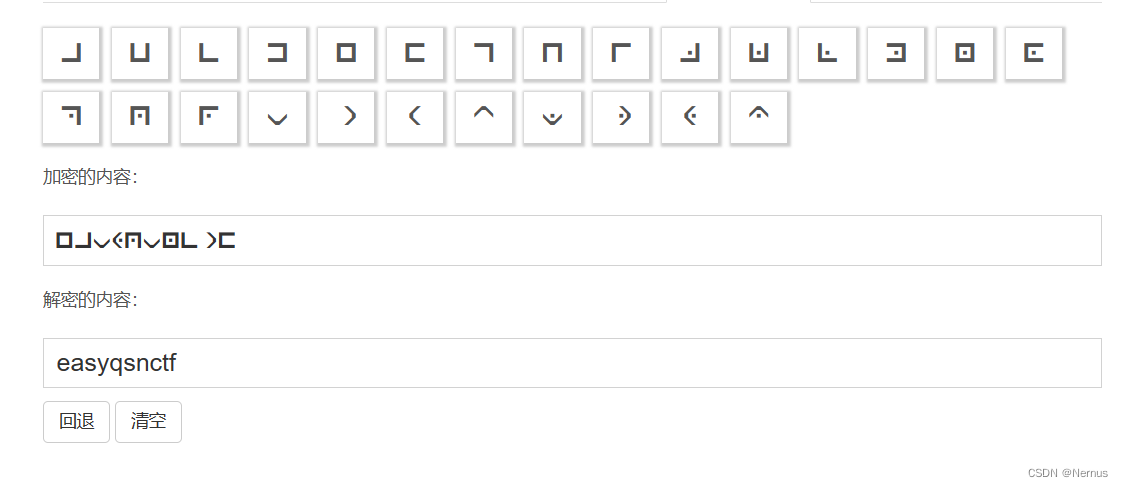
使用qsnctf{}包裹,得到flag
ez_log
题目提示:
注意:请将 key提交到页面内,flag提交到这里来!
打开环境
下载附件
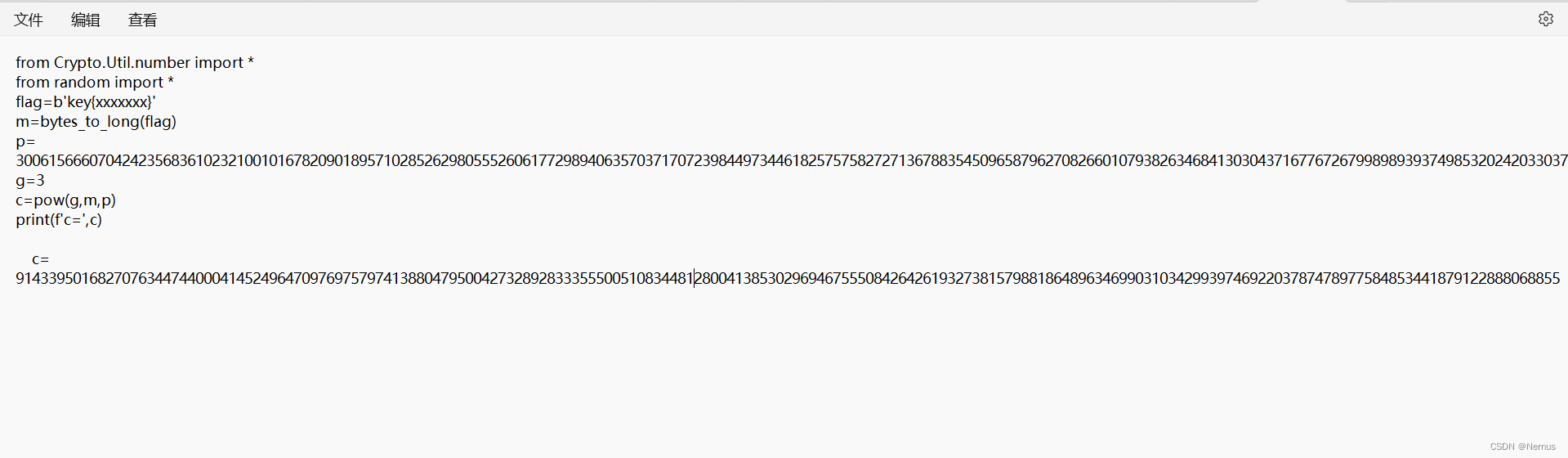
离散对数求解问题
逆着求m,对应log函数
bytes_to_long就相当于将字符串转为对应的十进制数,逆着为将得到的十进制计算转成十六进制,然后每两位对应一个ascii对应的值
使用sage解决
【SageMath】SageMath在Windows系统下的安装_sagemath下载-CSDN博客
SageMath的新手保姆使用教程-CSDN博客
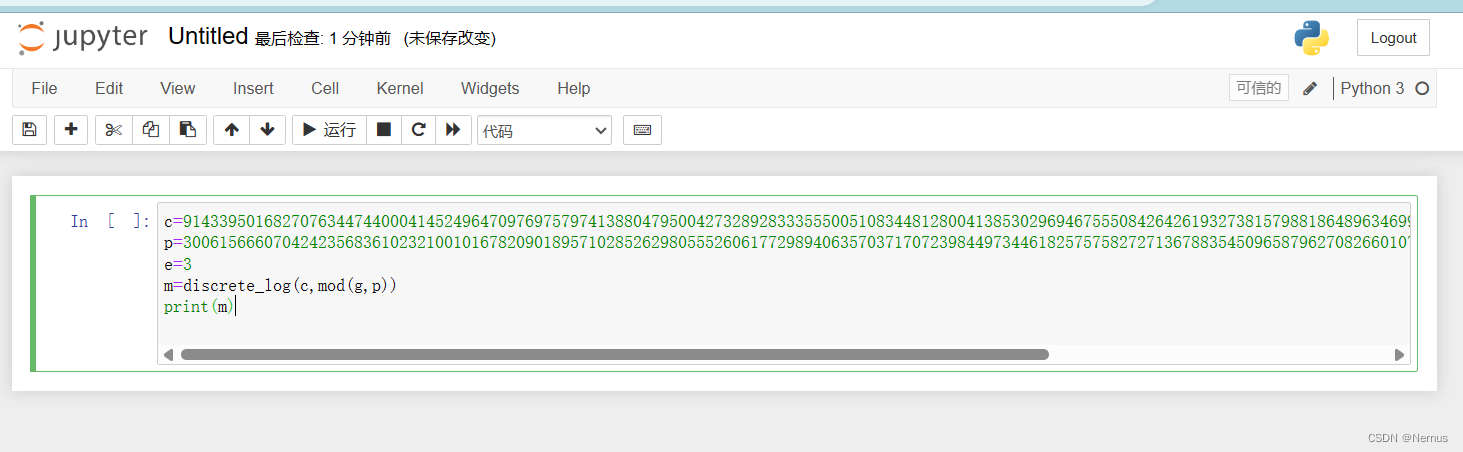
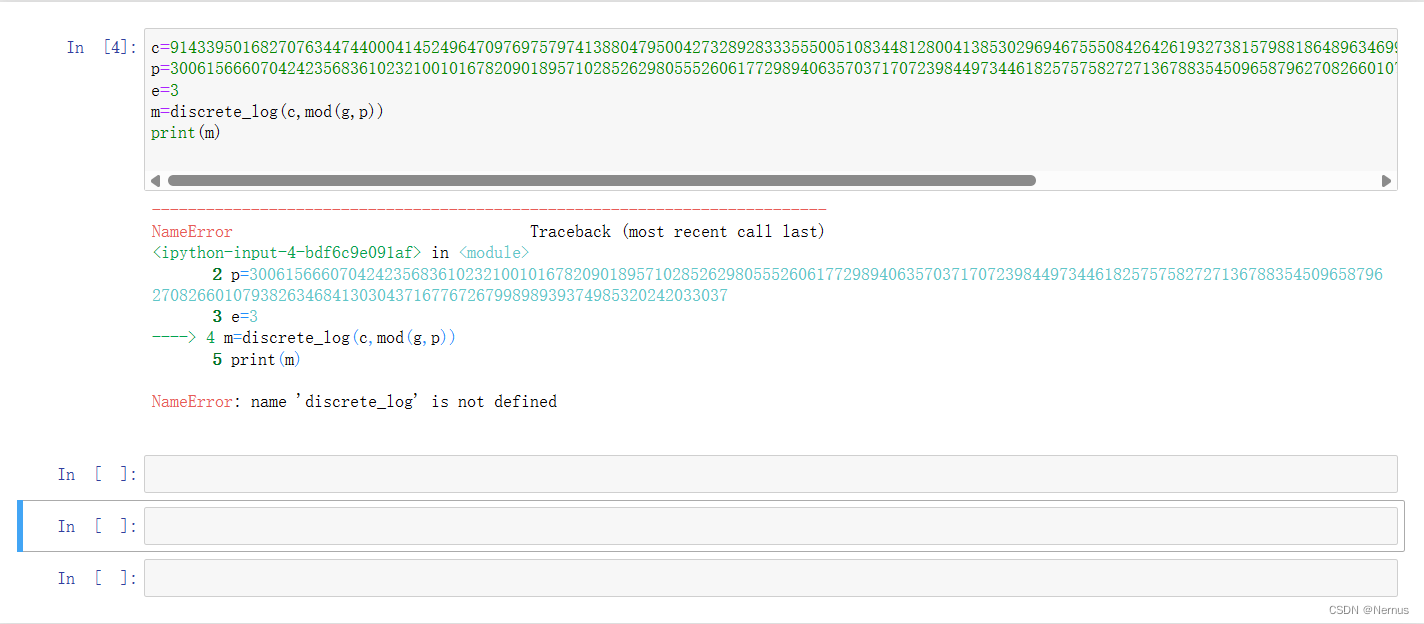
但是报错了
尝试编写脚本解码
from Crypto.Util.number import *
import gmpy2
c=
p=
e=
flag = discrete_log(Mod(c,p),Mod(g,p))
print(long_to_bytes(flag))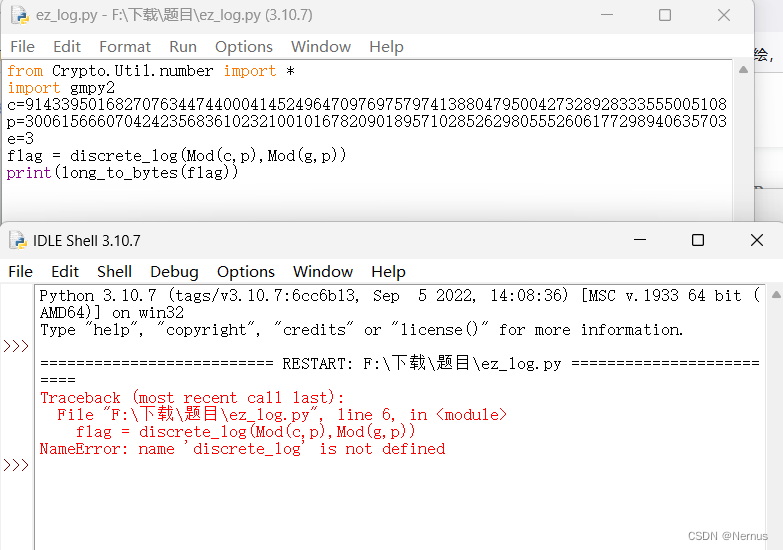
依旧报错,上网查找后仍未找到解决方法。
2024青少年ctf擂台挑战赛round1-ez_log-CSDN博客
解个方程
打开环境

下载附件
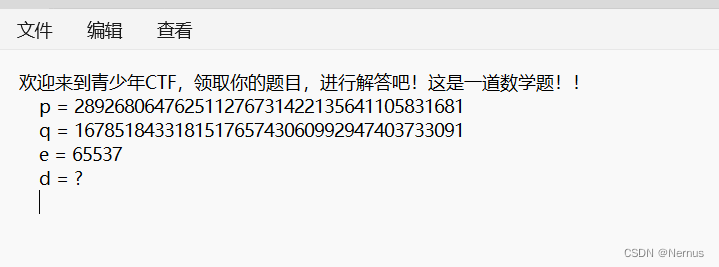
原理并不难,已知p,q,e求d。简单的rsa
编写脚本
import gmpy2
p =
q =
e =
d = gmpy2.invert(e,(p-1)*(q-1))
print (d)运行后得到d的值
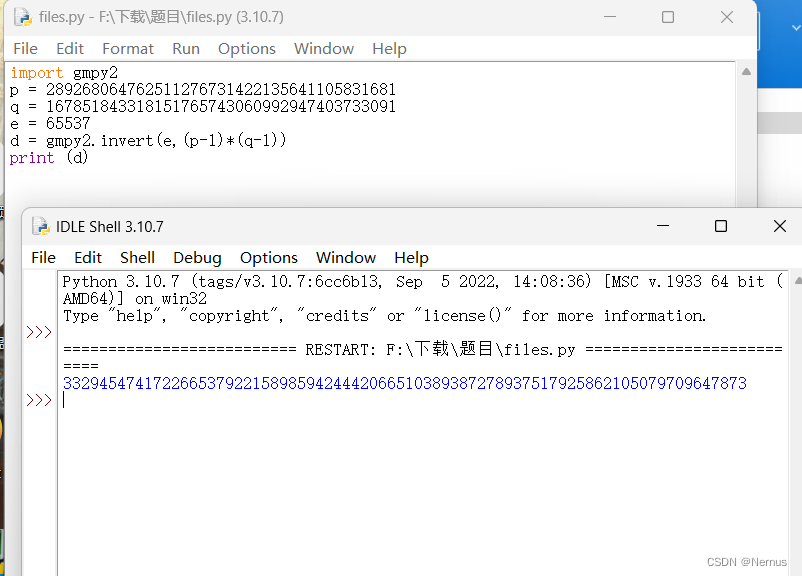
3329454741722665379221589859424442066510389387278937517925862105079709647873
提交d值后,得到flag

ezrsa

下载解压,打开附件
n分解出q、p、r,但是多因子解码不可信。
可以得出单个r,进行r的简单RSA计算
编写脚本
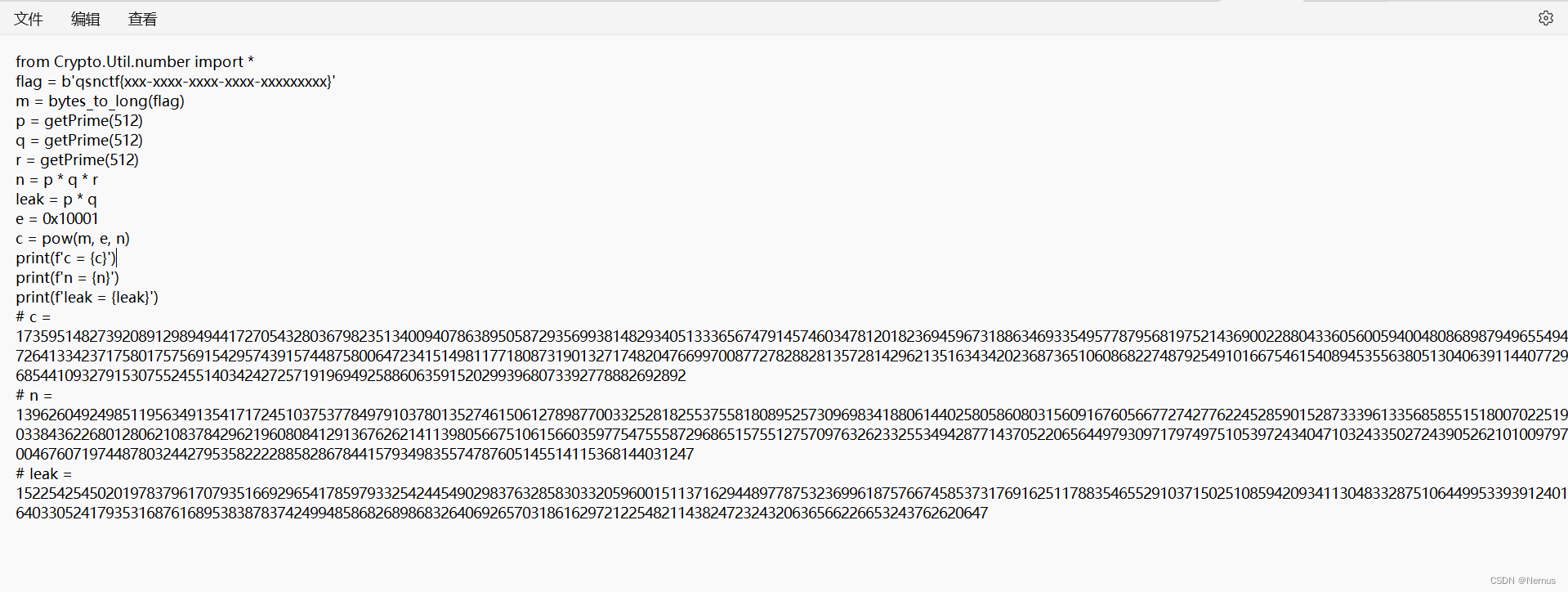
from Crypto.Util.number import *
import gmpy2
c = 173595148273920891298949441727054328036798235134009407863895058729356993814829340513336567479145746034781201823694596731886346933549577879568197521436900228804336056005940048086898794965549472641334237175801757569154295743915744875800647234151498117718087319013271748204766997008772782882813572814296213516343420236873651060868227487925491016675461540894535563805130406391144077296854410932791530755245514034242725719196949258860635915202993968073392778882692892
n = 1396260492498511956349135417172451037537784979103780135274615061278987700332528182553755818089525730969834188061440258058608031560916760566772742776224528590152873339613356858551518007022519033843622680128062108378429621960808412913676262141139805667510615660359775475558729686515755127570976326233255349428771437052206564497930971797497510539724340471032433502724390526210100979700467607197448780324427953582222885828678441579349835574787605145514115368144031247
leak = 152254254502019783796170793516692965417859793325424454902983763285830332059600151137162944897787532369961875766745853731769162511788354655291037150251085942093411304833287510644995339391240164033052417935316876168953838783742499485868268986832640692657031861629721225482114382472324320636566226653243762620647
e = 0x10001
r = n // leak
r=9170584408726584113673965972648240491689635118606416619099032606248549219208315227501144611402976054161705877934617690915635968224924300539749199425819801
phr = r - 1
d = gmpy2.invert(e,phr)
m = pow(c,d,r)
print(long_to_bytes(m))
运行
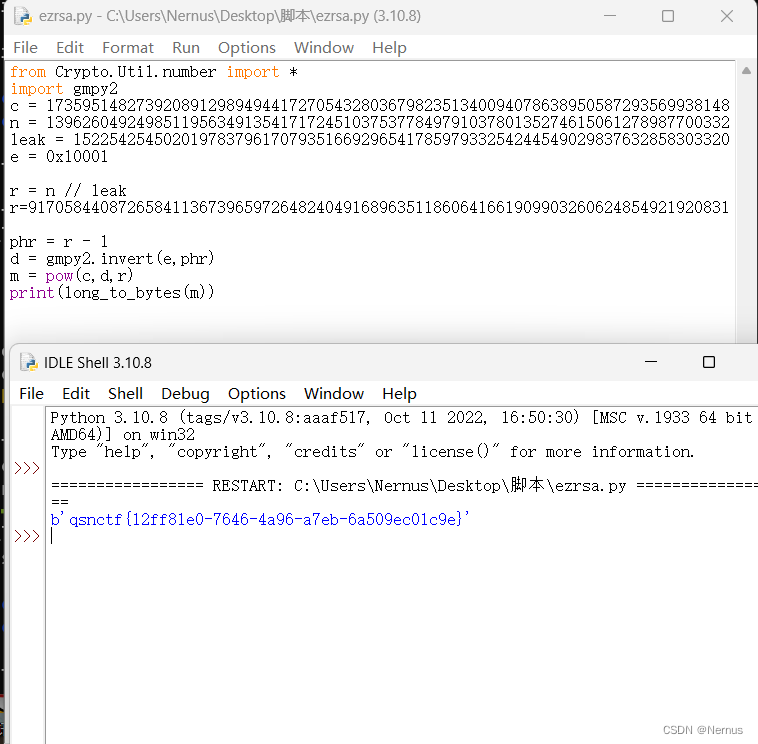
得到flag
qsnctf{12ff81e0-7646-4a96-a7eb-6a509ec01c9e}






![[数据集][目标检测]结直肠息肉内镜图像病变检测数据集13524张2类别](https://img-blog.csdnimg.cn/direct/63b910af03074b28b8f787ed922e6991.png)